what is the condition on b to guarantee ax = b is consistent

In linear algebra, Cramer'southward rule is a specific formula used for solving a organization of linear equations containing as many equations as unknowns, efficient whenever the organization of equations has a unique solution. This rule is named later Gabriel Cramer (1704–1752), who published the rule for an arbitrary number of unknowns in 1750. This is the virtually commonly used formula for getting the solution for the given system of equations formed through matrices. The solution obtained using Cramer's rule volition be in terms of the determinants of the coefficient matrix and matrices obtained from it past replacing i cavalcade with the column vector of the right-mitt sides of the equations.

Cramer's Rule Definition

Cramer's dominion is 1 of the important methods applied to solve a system of equations. In this method, the values of the variables in the system are to be calculated using the determinants of matrices. Thus, Cramer's rule is too known as the determinant method.

Cramer's Rule Formula

Consider a system of linear equations with due north variables x₁, ten₂, ten₃, …, xₙ written in the matrix grade AX = B.

Here,

A = Coefficient matrix (must be a square matrix)

X = Cavalcade matrix with variables

B = Column matrix with the constants (which are on the right side of the equations)

At present, nosotros have to notice the determinants every bit:

D = |A|, Dx_ane, Dx_ii, Dx_three,…, Dx_{due north}

Here, Dx_i for i = ane, 2, 3,…, n is the aforementioned determinant every bit D such that the column is replaced with B.

Thus,

x_ane = Dx₁/D; 10_ii = Dx₂/D; x₃ = Dx₃/D; ….; ten_n = Dx_n/D {where D is not equal to 0}

As well, try: Cramer'south Rule Calculator

Let's have a look at the formulas of Cramer's rule for 2×ii and 3×three matrices.

Cramer'southward Rule 2×two

Cramer's dominion for the 2×2 matrix is applied to solve the organisation of equations in ii variables.

Permit us consider two linear equations in two variables.

a_onex + b₁y = c_ane

a₂x + b_iiy = c_two

Let united states write these two equations in the form of AX = B.

\(\begin{array}{l}\begin{bmatrix} a_1 & b_1\\ a_2 & b_2 \terminate{bmatrix}\begin{bmatrix} x\\ y \finish{bmatrix}=\begin{bmatrix} c_1\\ c_2 \finish{bmatrix}\finish{array} \)

Here,

Coefficient matrix =

\(\brainstorm{array}{l}A=\begin{bmatrix} a_1 & b_1\\ a_2 & b_2 \end{bmatrix}\terminate{array} \)

Variable matrix =

\(\brainstorm{assortment}{fifty}X=\brainstorm{bmatrix} x\\ y \end{bmatrix}\end{array} \)

Constant matrix =

\(\begin{array}{50}B=\begin{bmatrix} c_1\\ c_2 \end{bmatrix}\stop{array} \)

\(\begin{array}{l}D=|A|=\begin{vmatrix} a_1 & b_1\\ a_2 & b_2 \end{vmatrix}=a_1b_2-a_2b_1\end{array} \)

And

\(\begin{assortment}{l}D_x=\begin{vmatrix} c_1 & b_1\\ c_2 & b_2 \finish{vmatrix}=c_1b_2-c_2b_1\finish{array} \)

\(\brainstorm{assortment}{l}D_y=\brainstorm{vmatrix} a_1 & c_1\\ a_2 & c_2 \finish{vmatrix}=a_1c_2-a_2c_1\end{array} \)

Therefore,

x = D_x/D

y = D_y/D

Learn: Determinant of a Matrix

Cramer's Dominion Example – 2×2

Question:

Solve the following system of equations using Cramer's rule:

2x – y = 5

x + y = four

Solution:

Given,

2x – y = v

10 + y = iv

Permit us write these equations in the form AX = B.

\(\begin{array}{l}\brainstorm{bmatrix} ii & -i\\ one& 1 \stop{bmatrix}\begin{bmatrix} ten\\ y \finish{bmatrix}=\begin{bmatrix} 5\\ four \end{bmatrix}\end{array} \)

Here,

\(\begin{array}{l}A=\begin{bmatrix} two & -one\\ one& 1 \stop{bmatrix}\finish{array} \)

\(\begin{array}{l}X=\begin{bmatrix} ten\\ y \end{bmatrix}\end{array} \)

\(\brainstorm{array}{l}B=\brainstorm{bmatrix} 5\\ 4 \terminate{bmatrix}\terminate{array} \)

Now,

D = |A|

\(\begin{array}{50}=\begin{vmatrix} 2 & -1\\ i& 1 \stop{vmatrix}\end{array} \)

= 2(1) – (-1)1

= 2 + 1

= 3 ≠ 0

So, the given system of equations has a unique solution.

\(\begin{array}{l}D_x=\begin{vmatrix} five & -1\\ iv& 1 \end{vmatrix}\stop{assortment} \)

= 5(1) – (-1)(four)

= v + 4

= nine

\(\brainstorm{array}{l}D_y=\begin{vmatrix} 2 & 5\\ 1& 4 \cease{vmatrix}\stop{array} \)

= 2(iv) – 5(1)

= viii – five

= 3

Therefore,

x = D_x/D = ix/three = 3

y = D_y/D = 3/iii = 1

Cramer's Rule iii×three

To find the Cramer's rule formula for a iii×three matrix, we need to consider the system of 3 equations with three variables.

Consider:

a₁ten + b_aney + c₁z = d₁

a₂10 + b₂y + c₂z = d_ii

a₃x + b_iiiy + c₃z = d₃

Permit us write these equations in the form AX = B.

\(\begin{array}{l}\begin{bmatrix} a_1 & b_1 & c_1\\ a_2& b_2 &c_2 \\ a_3& b_3 & c_3 \end{bmatrix}\begin{bmatrix} x\\ y\\ z \terminate{bmatrix}=\begin{bmatrix} d_1\\ d_2\\ d_3 \end{bmatrix}\end{array} \)

Now,

\(\begin{array}{l}D=|A|=\begin{vmatrix} a_1 & b_1 & c_1\\ a_2& b_2 &c_2 \\ a_3& b_3 & c_3 \stop{vmatrix}\cease{array} \)

And

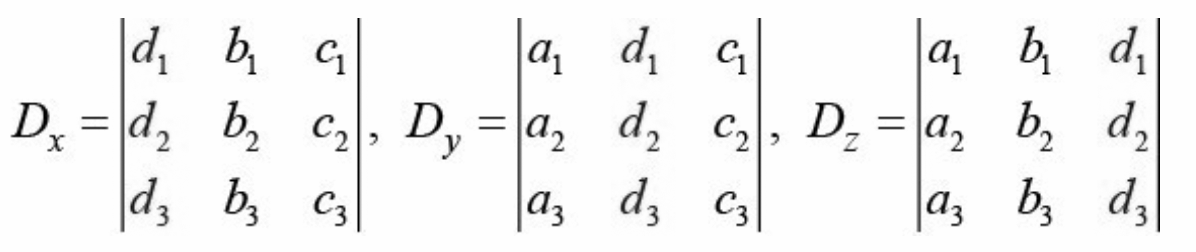
Therefore, ten = D_x/D, y = D_y/D, z = D_z/D; D ≠ 0

Get through the example given beneath to learn how to solve Cramer's rule for the 3×3 matrix.

Cramer's Dominion Example – iii×3

Question:

Solve the following organization of equations using Cramer'southward rule:

x + y + z =6

y + 3z = 11

x + z =2y or ten – 2y + z = 0

Solution:

Given,

ten + y + z =6

y + 3z = 11

ten + z =2y or ten – 2y + z = 0

Let us write these equations in the form AX = B.

\(\begin{array}{l}\begin{bmatrix} i & 1 &one \\ 0& ane & 3\\ 1 & -2 &1 \end{bmatrix}\brainstorm{bmatrix} 10\\ y\\ z \end{bmatrix}=\begin{bmatrix} 6\\ 11\\ 0 \terminate{bmatrix}\end{array} \)

Now,

\(\begin{array}{50}D=|A|=\brainstorm{vmatrix} 1 & 1 &i \\ 0& 1 & three\\ ane & -2 &1 \stop{vmatrix}=1(1 + 6)-1(0-3)+one(0-1) = 7+3-ane = 9\end{array} \)

D ≠ 0 so the given system of equations has a unique solution.

Also,

\(\brainstorm{array}{l}D_x=\begin{vmatrix} 6 & 1 &1 \\ 11& i & three\\ 0 & -2 &i \end{vmatrix}=6(ane+half-dozen)-i(11-0)+1(-22-0)=42-eleven-22=nine\finish{array} \)

\(\begin{array}{50}D_y=\brainstorm{vmatrix} 1 & six &1 \\ 0& 11 & three\\ 1 & 0 &1 \end{vmatrix}=i(11-0)-6(0-3)+i(0-xi)=eleven+xviii-11=18\end{assortment} \)

\(\begin{assortment}{l}D_z=\brainstorm{vmatrix} 1 & i &half dozen \\ 0& 1 & 11\\ 1 & -2 &0 \end{vmatrix}=1(0+22)-one(0-eleven)+6(0-1)=22+eleven-6=27\end{array} \)

Thus,

x = D_x/D = 9/9 = 1

y = D_y/D = 18/9 = 2

z = D_z/D = 27/9 = 3

Cramer'south Rule Conditions

In that location are sure conditions to applying Cramer's dominion for solving the given organization of equations. Some of them include the following:

• Cramer's rule fails for the arrangement of equations in which D = 0 since for finding the values of unknowns, D must be in the denominator and hence these values get undefined.
• Also, when D = 0, there will be ii possibilities for which:

  The system may have no solution.

The arrangement may have an infinite number of solutions.

From this, nosotros can say that at least 1 of the numerator determinants is a 0 (that means infinitely many solutions) or none of the numerator determinants is 0 (that ways no solution)

• If D ≠ 0, nosotros say that the organisation AX = B has a unique solution.

Thus, Cramer'south rule helps u.s. determine whether the given system has "no solution" or "infinite number of solutions", using the determinants we summate to apply the rule.

Cramer'south Rule Questions

1. Solve the post-obit system of equations by Cramer's rule:

   2x – 3y + 5z = 11

   3x + 2y – 4z = – 5

   x + y – 2z = – 3

2. Solve the following arrangement of linear equations using Cramer's rule:

   5x + 7y = -ii

4x + 6y = -three

1. The cost of four kg onion, 3 kg wheat and 2 kg rice is Rs 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is Rs 90. The cost of six kg onion 2 kg wheat, and three kg rice is Rs lxx. Discover the cost of each particular per kg by Cramer'south dominion.

Frequently Asked Questions on Cramer's Rule

What is Cramer'south rule in the matrix?

In matrices, Cramer's rule is used to find the solution of a system of linear equations in n variables.

What is Cramer's dominion also known as?

Cramer's dominion is too known as the determinant method.

Does Cramer'southward rule always work?

No, Cramer'south rule does not ever work. Every bit we know, information technology is applicative only when the given system of equations has a unique solution.

What is the limitation of Cramer'south rule?

The limitations of Cramer'southward rule are given below:
This dominion will non give the solution for the system of equations with infinite solutions and no solution.
When D = 0, Cramer's rule volition not give the values of unknowns.
It provides the results only when D ≠ 0.

In what condition does Cramer's rule fail?

When the determinant of matrix A in AX = B is equal to 0, Cramer's rule fails to provide the values of variables.

patellonarterfes.blogspot.com

Source: https://byjus.com/maths/cramers-rule/

Share this post